Example
The below example has been developed to illustrate the difference between the Deterministic Approach and the Stochastic Approach in retirement planning. The example will also help you in understanding how you can use this tool.
Step 1: Using the Deterministic Approach to Calculate Required Retirement Corpus
First, let us use the Deterministic Approach to calculate the required retirement corpus using the below assumptions:
- Annual Expenditure: INR 12 lakhs
- Equity Allocation: 50%
- Retirement Period: 360 months (30 years)
- Equity Return: 12% p.a.
- Debt Return: 7% p.a.
- Inflation: 5% p.a.
Based on the above inputs, the required retirement corpus is INR 1.97 crores.
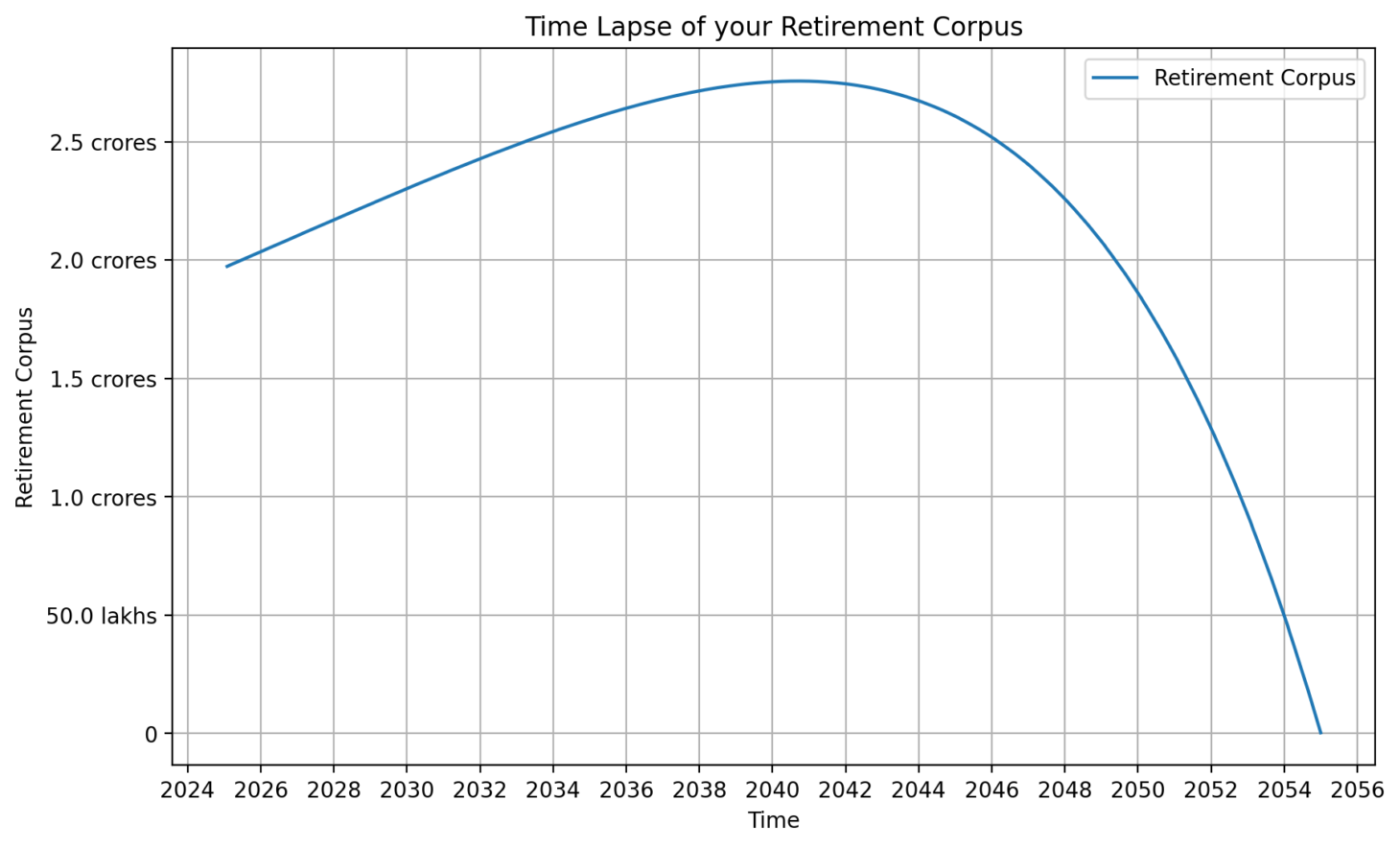
Figure 1: Corpus evolution using the Deterministic Approach
In the early years, the retirement corpus keeps increasing. This is because the income from the corpus more than offsets the retirement expenditure. However, since the expenditure grows with inflation, there comes a point of inflection at which the expenditure starts overshooting the income. Subsequent to this inflection point, the retiree starts eating into the principal component of their retirement corpus. However, the corpus exhausts itself only at the end of the retirement period.
The above planning, which works well on paper, can go horribly wrong, as it does not consider the sequence of return risk. To understand this, lets go to Step 2.
Step 2: Testing the Adequacy of the Estimated Retirement Corpus
To check the adequacy of the retirement corpus calculated in Step 1, we will now run simulations on the estimated corpus using the below assumptions:
- Annual Expenditure: INR 12,00,000 (Same as what we used above)
- Size of Retirement Corpus: INR 1.97 crores (Same as what we calculated above)
- Equity Allocation: 50% (Same as what we used above)
- Retirement Period: 360 months (30 years), (Same as what we used above)
- No. of Simulations: 3,000
The failure rate obtained from the simulations is 71%. This means that the retirement corpus calculated using the Deterministic Approach has a high chance of failing. This highlights the fact that typical retirement computations can be grossly inaccurate.
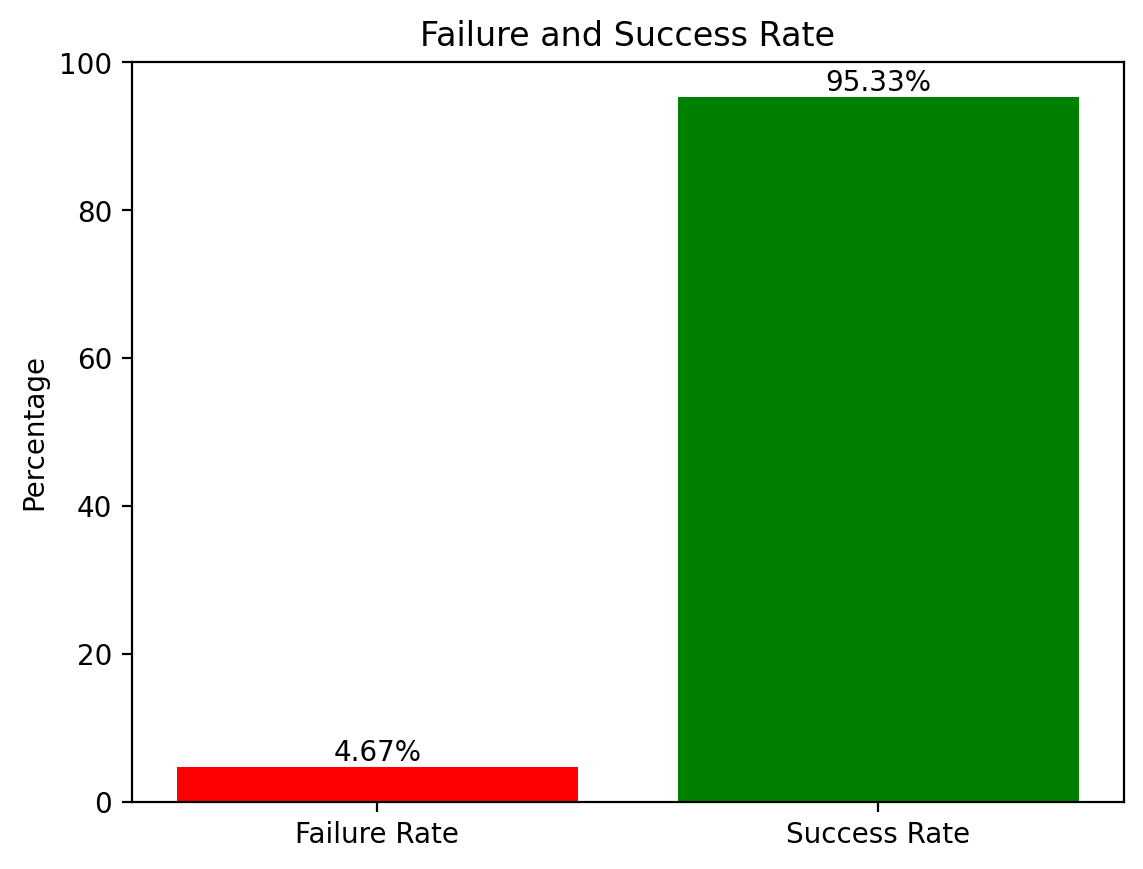
Figure 2: Simulation results showing high failure rate
You can also see below for a visual representation of the simulations run on the retirement corpus. As is evident, in several of the simulations, the retirement corpus ends negative, highlighting the inadequacy of the corpus calculated using the Deterministic Approach.

Figure 3: Multiple simulation paths showing corpus depletion
Step 3: Calculating the Required Retirement Corpus using the Stochastic Approach
The Stochastic method gives a more reliable estimate of the required retirement corpus. For this, we will use the below assumptions:
- Annual Expenditure: INR 12,00,000 (Same as what we used above)
- Equity Allocation: 50% (Same as what we used above)
- Retirement Period: 360 months (30 years), (Same as what we used above)
- No. of Simulations: 3,000
Under the Stochastic method, the code will try out different expenditure cover ratios to find the required retirement corpus such that the failure rate is close to 5 percent.

Figure 4: Stochastic simulation results
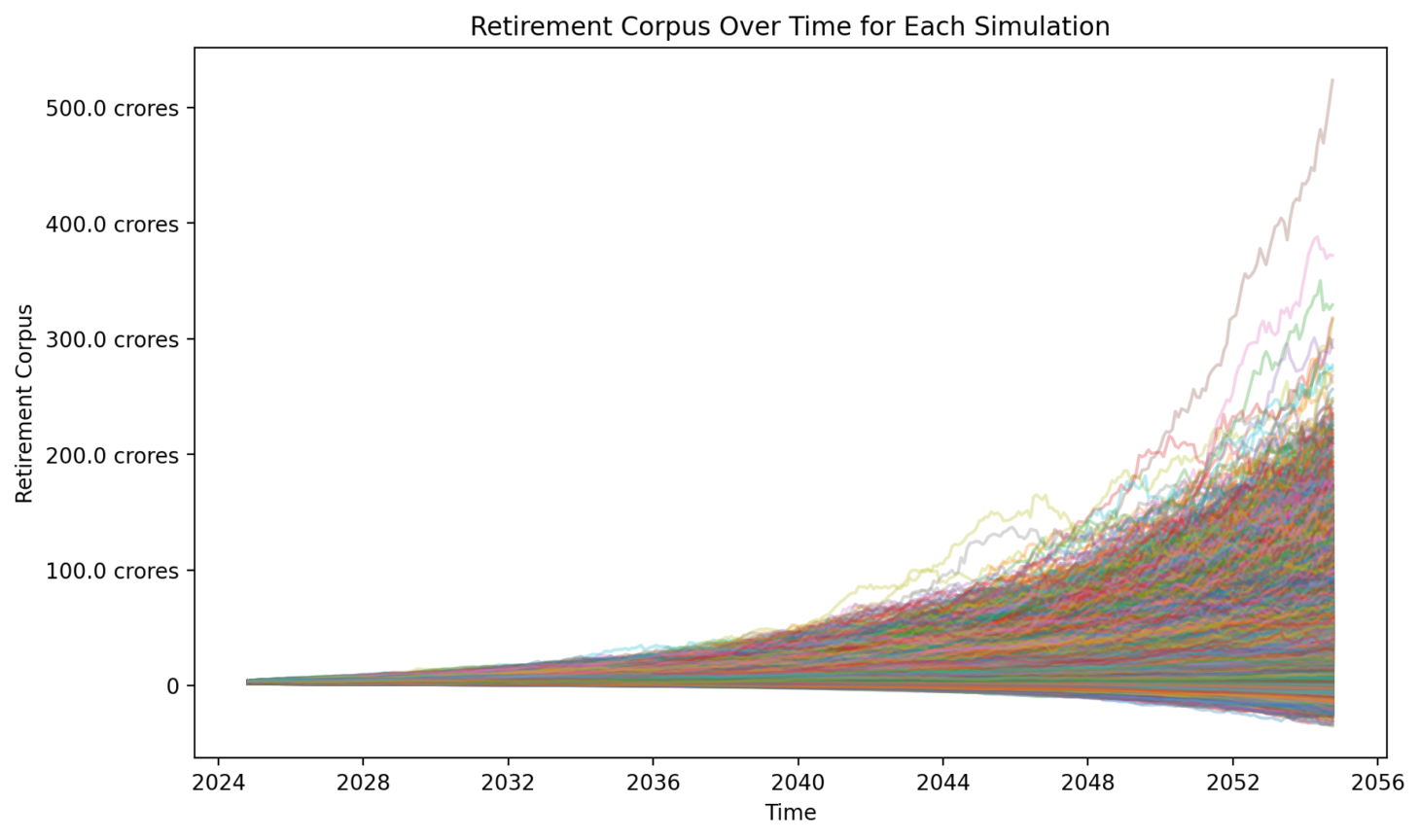
Figure 5: Distribution of simulation outcomes
In our case, the required retirement corpus under the Stochastic method is INR 3.78 crores, which is significantly higher than the corpus calculated using the Deterministic Approach. A retirement corpus of INR 3.78 crores will entail a failure rate of less than 5 percent.